Moving Averages
I discuss moving or rolling averages, which are algorithms to compute means over different subsets of sequential data.
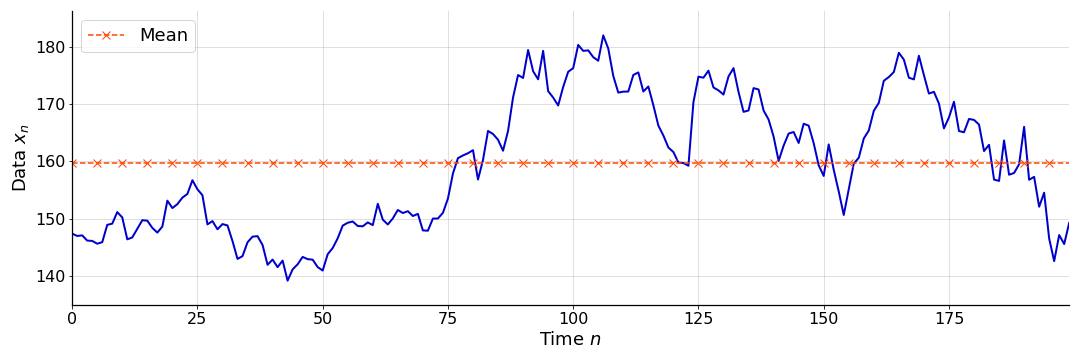
A moving average, sometimes called a rolling average, is a sequence of averages, constructed over subsets of a sequential data set. Moving averages are commonly used to process time series, particularly to smooth over noisy observations. For example, consider the noisy function in Figure
While moving averages are fairly simple conceptually, there are details that are useful to understand. In this post, I’ll discuss and implement the cumulative average, the simple moving average and the weighted moving average. I’ll also discuss a special case of the weighted moving average, the exponentially weighted moving average.
Cumulative average
Consider a sequential data set of
These data do not need to be a time series, but they do need to be ordered. For simplicity, I will refer to the index
Perhaps the simplest way to make the point estimate in Figure
The effect is a sequence of mean estimates that account for increasingly more of the data. See Figure
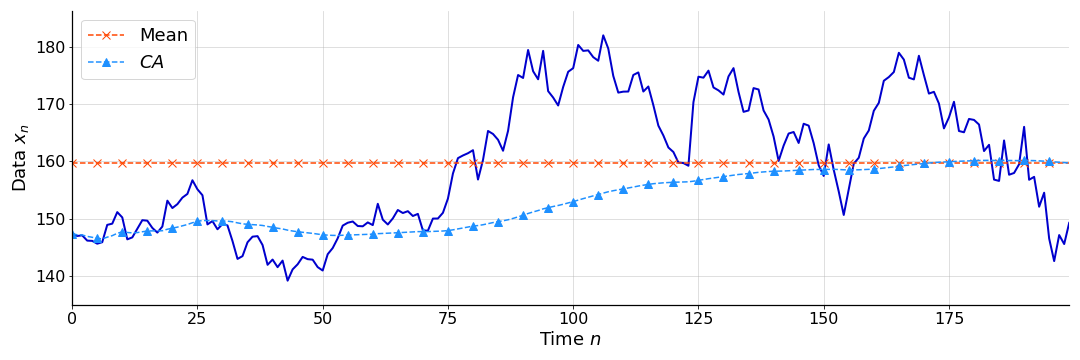
We can implement a CA in Python as follows:
def ca(data):
"""Compute cumulative average over data.
"""
return [mean(data[:i]) for i in range(1, len(data)+1)]
def mean(data):
"""Compute mean of data.
"""
return sum(data) / len(data)
Notice, however, that re-computing the mean at each time point is inefficient. We could simply undo the normalization of the previous step, add the new datum, and then re-normalize. Formally, the relationship between
This results in a faster implementation:
def ca_iter(data):
"""Compute cumulative average over data.
"""
m = data[0]
out = [m]
for i in range(1, len(data)):
m = ((m * i) + data[i]) / (i+1)
out.append(m)
return out
As we’ll see, this idea of iteratively updating the mean, rather than fully recalculating it, is typical in moving average calculations.
Simple moving average
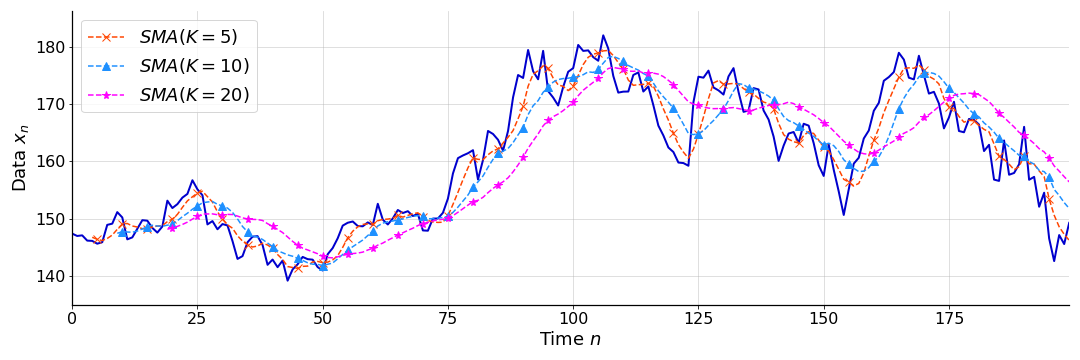
While the CA in Figure
At each time point
Note that based on the definition in Equation
Following the convention used by Pandas, I’ll define
See Figure
In Python, a simple moving average can be computed as follows:
nan = float('nan')
def sma(data, window):
"""Compute a simple moving average over a window of data.
"""
out = [nan] * (window-1)
for i in range(window, len(data)+1):
m = mean(data[i-window:i])
out.append(m)
return out
However, there is a trick to computing SMAs even faster. Since the denominator never changes, we can update an existing mean estimate by subtracting out the datum that “falls” out of the window, and adding in the latest datum. This results in an iterative update rule,
In Python, this faster implementation is:
def sma_iter(data, window):
"""Iteratively compute simple moving average over window of data.
"""
m = mean(data[:window])
out = [nan] * (window-1) + [m]
for i in range(window, len(data)):
m += (data[i] - data[i-window]) / window
out.append(m)
return out
(Obviously, the code in this post is didactic, ignoring edge conditions like ill-defined windows.)
Weighted moving average
An obvious drawback of a simple moving average is that, if our sequential data changes abruptly, it may be slow to respond because it equally weights all the data points in the window. A natural extension would be to replace the mean calculation with a weighted mean calculation. This would allow us to assign relative importance to the observations in the window. This is the basic idea of a weighted moving average (WMA). Thus, each observation in the window has an associated weight,
and these are applied consistently (i.e. in the same order) as the window moves across the input. Formally, a weighted moving average is
Note that this definition is agnostic to the specific weighting scheme used, and that the number of weights can grow with the number of observations (
For example, we could use weights that emphasize the most recent datum, e.g. by decaying linearly with time (
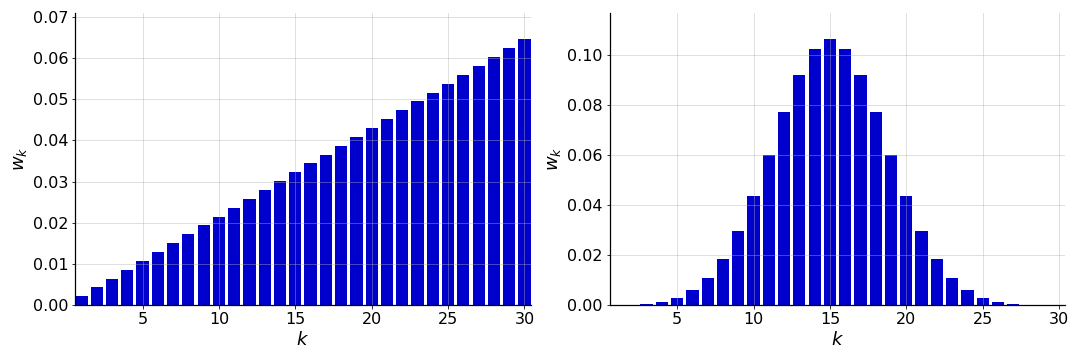
See Figure
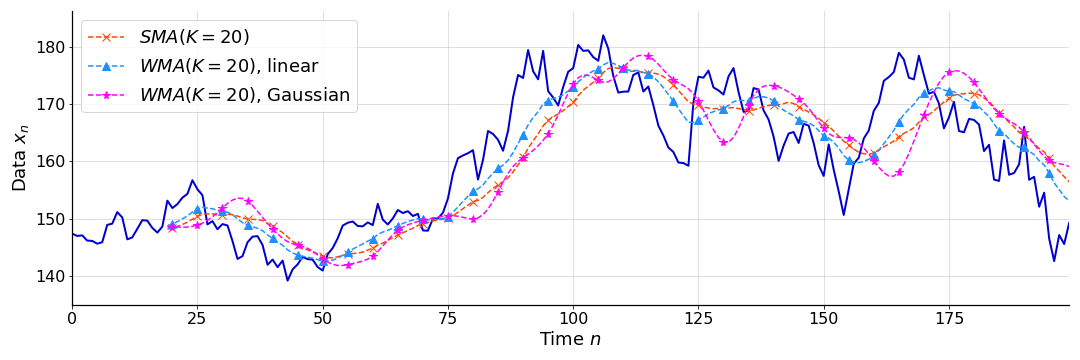
In Python, a naive WMA can be implemented as follows:
def wmean(data, weights):
"""Compute weighted mean of data.
"""
assert len(data) == len(weights)
numer = [data[i] * weights[i] for i in range(len(data))]
return sum(numer) / sum(weights)
def wma(data, weights):
"""Compute weighted moving average over data.
"""
window = len(weights)
out = [nan] * (window-1)
for i in range(window, len(data)+1):
m = wmean(data[i-window:i], weights)
out.append(m)
return out
I call this “naive” because it treats the weights as a moving window, which is an unnecessary constraint. As I mentioned above, the size of the window can grow with the number of observations. As with an SMA, there are tricks to computing WMAs even faster using iterative updates. However, the algorithmic details depend on the choice of weights. We’ll see one iterative update rule with exponentially decaying weights (below).
Exponential moving average
A poplar choice of WMA weights are ones that decay exponentially (Figure
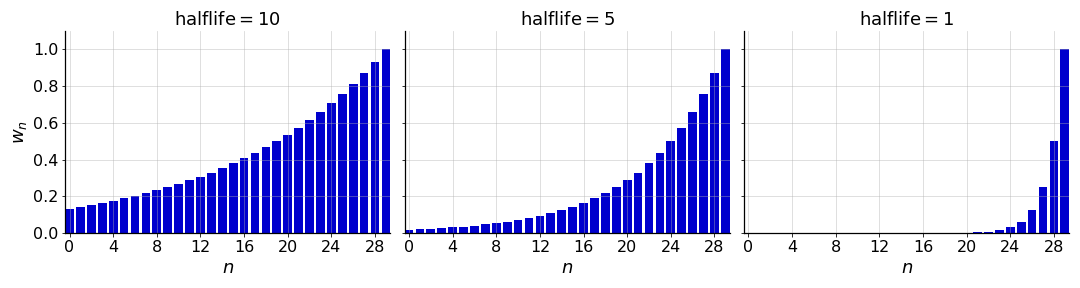
As a reminder, let
See my previous post on exponential decay as needed. Note that in my previous post, I denoted the decay rate as
Given the various parameterizations, there are many ways we could implement EWMAs, and each parameterization lends itself to a different iterative updating scheme. Clearly, discussing each in turn would be too tedious. Thus, I’ll narrow the discussion in the following way: first, I’ll explain EWMA using the halflife parameterization, which is the most natural in my mind. I like halflives because they are in the natural units of the process (e.g. halflife in hours for data that is hourly). I won’t refine this much, though. Instead, I’ll switch to discussing EWMA using the rate parameterization (using
Halflife parameterization
Recall that the halflife of exponential decay is the value in the domain at which the function reaches half of its initial value. Since exponential decay never reaches zero, the number of weights in an EWMA equals the number of observations so far (
Obviously, this equation depends on my notation. If you assumed that
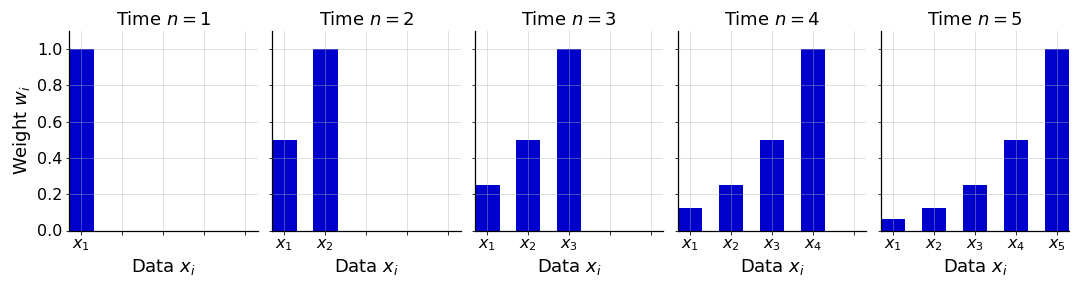
As I mentioned, in my mind, halflife is an intuitive parameter because it is in the natural units of the process. A shorter halflife means the EMA is more reactive to changes in data, while a longer halflife means that more historical data is considered for longer. So a bigger halflife means more smoothing. See Figure
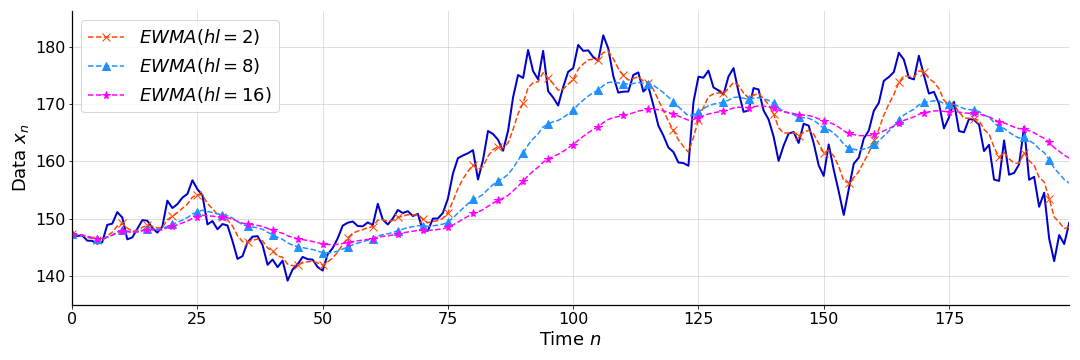
In Python, an EWMA can be implemented as follows:
def ewma_hl(data, halflife):
"""Compute exponentially weighted moving average with halflife over data.
"""
weights = [(1/2)**(x/halflife) for x in range(len(data), 0, -1)]
out = []
for i in range(1, len(data)+1):
m = wmean(data[:i], weights[:i])
out.append(m)
return out
Notice that I simply construct a set of exponentially decaying weights at the start, and then index into that set. This works for a subtle reason: since exponential decay is memoryless in the sense that the function decays as a fraction of its current quantity, the set of weights applied inside the weighted mean calculation (wmean) are always correct because they are normalized. If the un-normalized magnitude of the weights mattered, this implementation would not work.
Smoothing factor parameterization
Now let’s explore EWMAs in terms of the rate or smoothing factor adjust parameter.
To be clear, I’m not quite sure why the un-adjusted algorithm is discussed so often, since it technically incorrect and since both the halflife-parameterized algorithm and the adjusted EWMA are both easy to understand and correct. However, I’ve decided to discuss it simply since I have seen the un-adjusted formulation many times and never quite understood it. (When you see it, you should ask yourself why it is correct; in fact, it is not!)
Un-adjusted EWMA. A commonly discussed iterative update rule is the following,
Wikipedia cites the National Institute of Standards and Technology website, which in turn cites (Hunter, 1986) for this rule. We’ll investigate what Equation
Now let’s rewrite the update rule in Equation
In other words, the next predicted value in the time series is the current predicted value in the time series, plus some fraction of the error between what we observed and what we predicted. If
Either way, to quote (Hunter, 1986),
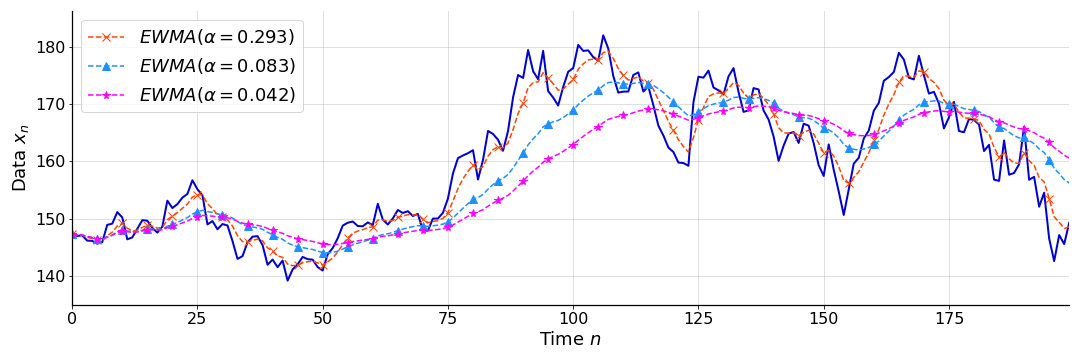
Now that we have some intuition for this formulation, let’s ask ourselves the obvious question: how does Equation
Note that we can distribute the
Here, we can see why Equation
Note that we are computing the weighted mean on the fly, meaning that these weights must sum to unity. Using basic properties of geometric series, we can verify this:
So this approach is reasonable. However, the weight associated with the first datum is incorrect. It should be
Adjusted EWMA. The correct update rule is the following:
Here, we update each datum with the weight
And we normalize the calculation at each time point by dividing by the sum of the weights. It’s pretty easy to see that both the numerator and denominator in Equation
This gives us a fast, iterative algorithm to exactly compute an EWMA online. In my mind, Equation
In Python, an EWMA with smoothing factor
def ewma_alpha(data, alpha):
num = data[0]
den = 1
out = [num/den]
for i in range(1, len(data)):
num = data[i] + (1 - alpha) * num
den = 1 + (1 - alpha) * den
out.append(num/den)
return out
This is the code that is used to produce Figure
Switching parameterizations
As a final comment, it’s useful to be able to switch to between the halflife and smoothing parameterizations. In my post on exponential decay, I showed that the smoothing factor
Later in the post, I also showed that halflife is related to decay in the following way:
Using these two equations, we can easily solve for
These operations are useful when you want to work in a particular parameterization that is not supported by a given EWMA implementation.
- Hunter, J. S. (1986). The exponentially weighted moving average. Journal of Quality Technology, 18(4), 203–210.